интервал на доверие за оценка на средната (вариацията е известно) в MS Excel - съвместим с Microsoft
MS EXCEL конструира доверителен интервал за изчисляване на средните стойности на разпределението в случай на известна стойност на дисперсията.
Статистика, вземане на проби за дистрибуция и точкови оценки в MS EXCEL дава определение за крайният резултат за параметър разпределение (точка оценител). Въпреки това, поради случайна точка приблизителна стойност за вземане на проби не съвпада с оценявания параметър и по-разумно да се посочи обхвата, в който параметърът може да бъде неизвестен в наблюдавано проба x1 на. x2. хп. Ето защо целта на използването на доверителни интервали е възможно да се отърве от несигурността и да дава възможност за по-полезни статистически извод.
Забележка. Процес, обобщаващ проба данни. което води до по вероятностен изявление за цялото население. Статистическа нарича терминал (статистически извод).
TIP. За изграждането на доверителния интервал, ние трябва да знаем следните понятия:
За съжаление, интервалът, в който неизвестен параметър може да бъде съвпада с възможно най-голяма гама от вариации на този показател, тъй подходящия избор. и следователно параметър за оценка. Вие може да се приготви с ненулева вероятност. Поради това, намирането на граници е необходимо да се ограничи промени на неизвестен параметър с предварително определена вероятност по-рано.
Определение: доверителен интервал се нарича интервал от случайна променлива kotoryys промени дадени вероятност ще покрие истинската стойност на очакваните параметър разпределение.
Това се нарича вероятността за дадено ниво на доверие (или доверителна вероятност).
Обикновено се използва стойност доверие ниво от 90%; 95%; 99%, най-малко 99,9% и т.н. Например, urovendoveriya 95% означава, че едно събитие, чиято вероятност 1-0,95 = 5%, изследователят счита, че е малко вероятно или невъзможно.
Забележка: Вероятността за това събитие се нарича допълнително ниво на значимост или грешка от първи вид. За подробности вижте. Член Ниво на значимост и надеждност в MS Excel.
Разбира се, изборът на нивото на доверие зависи изцяло от задача. По този начин, степента на доверие и придружаване до надеждността на самолета, разбира се, трябва да бъде по-висока от степента на доверие купувач в надеждността на електрическата крушка.
Изявление на проблема
Да приемем, че от популация с нормално разпределение получен размер проба п. Предполага се, че стандартното отклонение на това разпределение е известна. Необходимо е въз основа на тази проба за оценка на неизвестен средната стойност на разпределение (μ, очакването) и изграждане на съответния dvuhstoronniydoveritelny интервал.
момент за оценка
Както знаем от централната лимит теорема. статистика

Забележка: Какво да правите, ако искате да се изгради доверителен интервал в случай на разпределение, което не е yavlyaetsyanormalnym? В този случай, идва да помогне на централната лимит теорема. който гласи, че за достатъчно голям размер проба п от разпределението на не yavlyayuschemsyanormalnym. селективна дистрибуция на статистика HSR приблизително ще съответства на нормално разпределение с параметри N (μ; σ 2 / п).
Така че, точка otsenkasrednegoznacheniya разпределение имаме - това е средната стойност на извадката. т.е. XCP. Сега за доверителния интервал.
Строителство доверителен интервал
Обикновено ние знаем, разпределението и неговите параметри, можем да изчислим вероятността случайна променлива ще отчита стойността на определената ни интервал. Сега ние правим точно обратното: ние откриваме диапазона, в който случайна променлива ще падне с определена вероятност. Например, свойствата на нормалното разпределение е известно, че с вероятност от 95%, случайна променлива разпределени нормално. попада в обхвата от около +/- 2 стандартни отклонения от средната стойност (вж. статия за нормално разпределение). Този интервал, ще служи като прототип за доверителния интервал.
Сега ние трябва да разберем, ако знаем разпределението, за да се изчисли този интервал? За да се отговори на въпроса, че трябва да се уточни формата на разпределението и неговите параметри.
форма разпределение знаем - това е нормално разпределение (не забравяйте, че ние говорим за селективна raspredeleniistatistikiHsr).
параметър μ е неизвестен (тя просто трябва да бъде изчислен въз основа на доверителен интервал), но ние имаме своя резултат XCP изчислява въз основа на извадка, която може да се използва.
Вторият параметър - стандартното отклонение на srednegobudem за вземане на проби приема известен. тя е равна на сигма / √n.
защото ние не знаем μ, тогава ние ще изгради набор от +/- 2 стандартни отклонения от средната стойност не е така. както е известно от своя HSR оценка. Т.е. при изчисляване на доверителен интервал ние не приемаме, че HSR попада в диапазон +/- 2 стандартни отклонения от μ с вероятност от 95%, а ние приемаме, че интервалът +/- 2 стандартни отклонения от HSR с вероятност от 95% ще обхване μ - означава общите популацията, от която е взета пробата. Тези две твърдения са еквивалентни, но второто твърдение ни дава възможност за изграждане на доверителни интервали.
В допълнение, въведете стойност: случайна променлива разпределени нормално. с 95% вероятност в интервала 1,960 +/- стандартни отклонения, отколкото +/- 2 стандартни отклонения. Това може да се изчислява при използване на формулата NORM.ST.OBR = ((1 + 0,95) / 2). см. Пример файла лист интервал.

Сега можем да формулираме вероятностна изявление, че ще ни служат за формиране на доверителния интервал:
"Възможността, че средната стойност на населението е средната стойност на извадката в рамките на 1,960" на извадката означава стандартно отклонение ". равно на 95%. "
Стойността на вероятност, споменатият одобрение, името има специален ниво на доверие, което е свързано с α ниво на значимост (а) от прост ниво на експресия на доверие 1 = -α. В този случай, алфа на ниво на значимост = 1-0,95 = 0,05.
Сега, въз основа на това, че вероятността изявления пишете израза за изчисляване на доверителния интервал:
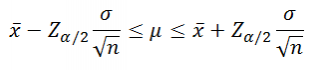
Забележка. Горна α / 2 квантил определя ширината на доверителния интервал, в стандартната otkloneniyahvyborochnogo среда. Разпределението на горната α / 2-kvantilstandartnogonormalnogo е винаги по-голяма от 0, което е много удобно.
В този случай, α = 0,05, горната α / 2-частици са 1960. За други нива на значимост α (10%, 1%) по-висок α / 2 kvantilZα / 2 може да бъде изчислена като се използва формулата NORM.ST.OBR = (1-α / 2), или ако нивото на доверие е известна. NORM.ST.OBR = ((1 + ur.doveriya) / 2).
Обикновено в изграждането на доверителни интервали за оценките на средната стойност се използва само горната a / 2-квантил и не използвайте долната α / 2 квантил. Това е възможно, защото разпределението standartnoenormalnoe е симетричен около оста х (разпространението му плътност е симетрично спрямо средната стойност, т.е. 0). Следователно, не е необходимо да се изчисли нисш α / 2-квантил (наречен просто a / 2 квантил) като тя е равна на горната α / 2-квантил със знак минус.
Припомнете си, че, независимо от формата на разпределението на съответния х HSR случайна стойност се разпределя priblizitelnonormalno N (μ; σ 2 / N) (. Виж статията за CLT). Следователно, като цяло, по-горе израз за доверителния интервал е само приближение. Ако стойността на х е нормално разпределение N (μ; σ 2 / п), след експресията на доверителния интервал е точна.
Изчисляване на доверителния интервал, в MS EXCEL
Ние решаване на проблема.
Електронната време за реакция компонент на входния сигнал е важна характеристика на устройството. Инженерът иска да построи доверителен интервал за средното време за отговор при 95% ниво на доверие. инженер знае от предишен опит, че стандартното отклонение на времето за реакция е 8 милисекунди. Известно е, че времето за реакция за оценка на инженер направени 25 измервания, средната стойност на 78 мсек.
Решение. Инженерът иска да знае времето за реакция на електронното устройство, но той осъзнава, че времето за реакция не е фиксирана, тъй като случайна променлива, която има своя собствена дистрибуция. Така че, най-доброто, че той може да се надяваме, е да се определят параметрите и формата на тази дистрибуция.
За съжаление, състоянието на разпределението на отговор задача време на формуляр ние не знаем (тя не трябва да бъде нормален). Средно, т.е. очакване. Това разпределение е неизвестен. Известно е само чрез стандартно отклонение си σ = 8. Затова, въпреки че ние не можем да се изчисли вероятността и изграждане на доверителен интервал.
Въпреки това, независимо от факта, че ние не знаем vremeniotdelnogo разпределение отговор. Ние знаем, че в зависимост от CLT. raspredeleniesrednego селективен време за реакция е приблизително нормалния (приемем, че са изпълнени условията PTC, тъй като размерът на пробата е достатъчно голям (п = 25)).
Освен това, средната стойност на това разпределение е средна стойност на единица отговор на разпределение, т.е. μ. Стандартно отклонение от това разпределение (σ / √n) може да се изчисли чрез формулата = 8 / SQRT (25).
Известно е също така, че точка цената инженер на параметъра μ е равно на 78 мсек (HSR) се получава. Ето защо, сега можем да се изчисли вероятността, защото ние знаем формата на разпределението (нормален) и неговите параметри (XCP и σ / √n).
Инженерът иска да знае очакване μ разпределението на времето за реагиране. Както бе споменато по-горе, това е μ равно на средната стойност на разпределението на вземане на проби от Средното време за отговор. Ако се използва нормално разпределение N (HSR; σ / √n), след това желания ц ще бъде в границите +/- 2 * σ / √n с вероятност от около 95%.
Нивото на значимост е равна 1-0,95 = 0.05.
И накрая, ние откриваме, че лявата и дясната граница на доверителния интервал.
Лява граница = 78 NORM.ST.OBR (1-0,05 / 2) * 8 / SQRT (25) = 74.864
Точно граница = 78 + NORM.ST.OBR (1-0,05 / 2) * 8 / SQRT (25) = 81.136
Лява граница = NORM.OBR (0.05 / 2; 78; 8 / SQRT (25))
Точно граница = NORM.OBR (1-0,05 / 2; 78; 8 / SQRT (25))
Отговор. доверителен интервал 95% доверителен интервал и σ = 8 мсек е 78 мсек +/- 3136.
Например файлът за форма на лист създаден Sigma известен за изчисляване и конструиране dvuhstoronnegodoveritelnogo интервал за произволни проби с σ и определете степента на значимост.

DOVERIT.NORM функция ()
Ако пробата стойности са в В20 в диапазон: B79. и ниво на значимост равна на 0,05; формула MS EXCEL:
= Средна (В20: В79) -DOVERIT.NORM (0,05; σ; COUNT (В20: В79))
върнете лявата граница на доверителния интервал.
Същата тази граница може да бъде изчислена по формулата:
= Средна (В20: В79) -NORM.ST.OBR (1-0,05 / 2) * σ / SQRT (COUNT (В20: В79))