Образователен портал на ТСУ
Вътрешно наричат тези колебания, които се срещат в колебателно система под действието на външни сили периодично променящи се (ние го наричаме движеща сила). Нека движеща сила варира в зависимост от хармоничен закон
При събирането на уравненията на движение е необходимо да се разгледа, освен движеща сила, също на силите, които действат в системата в режим на свободно вибрации, т.е. ,. Quasielastic сила и силата на съпротивление. Ако приемем, че колебанията на достатъчно малки, ще продължат да се разглеждат сила пропорционална на степента на съпротива. Тогава уравнението на движение може да се запише по следния начин:
Разделяне това уравнение от m и изместване членове с х и х към лявата страна, ние получаваме нехомогенни линеен втори ред диференциално уравнение:
при което - затихване коефициент, на естествената честота на трептене на системата.
Както е известно от теорията на диференциални уравнения, общото решение на нехомогенни уравнение е сумата от общия разтвор на съответното хомогенно уравнение и конкретен разтвор на нехомогенни уравнение. ние вече знаем общото решение на хомогенното уравнение [виж. функция (73,10) е общото решение на уравнение (73.2)]. Той има формата
Функцията (75.9) в размер на (75.3) дава общото решение на уравнение (75.2), в който се описва поведението на системата при принудени трептения. Терминът (75.3) играе важна роля само в началния етап на процеса, така наречените създаване трептения (фиг. 188)

С течение на времето, поради експоненциалния фактор за ролята на срока (75.3) все повече се намалява, и достатъчно време, тя може да се пренебрегне, което запазва само термина в разтвора (75.9).
По този начин, функцията (75.9) описва стабилно принудени трептения. Те представляват хармонично трептене с честота равна на движеща сила. Амплитудата (75.7) пропорционално на амплитудата на принудени трептения на движеща сила. За тази осцилаторна система (и определени), амплитудата зависи от честотата на движеща сила. Принудително вибрации на латентна фаза от изтласкващата сила, при което стойността на забавяне също зависи от честотата на движеща сила [вж. (75.8)].
Зависимостта на амплитудата на принудени трептения на честотата на движещата сила причини ", които по някакъв специфичен за дадена амплитуда система честота на трептене достига максималната си стойност, вибрационната система е особено чувствителен към действието на движеща сила при тази честота. Това явление се нарича резонанс, и съответната честота - резонансната честота.
За определяне на резонансната честота. Трябва да се намери максимума на функцията (75.7) или, еквивалентно, минимум на експресията при корен квадратен в знаменател. Разнообразяване на този израз с уважение и се равнява на нула, ние получаваме условието, което определя:
От (75.12) следва, че при липсата на устойчивост на околната среда на амплитуда резонанс ще стане безкрайно. Според (75,11), резонансна честота при същите условия (в) съвпада с естествената честота на трептене на системата.
Зависимостта на амплитудата на принудени трептения на честотата на силата на водача (или еквивалентно camoe от честотата на трептене) е показана графично на Фиг, 189. Отделни кривите на графиката съответстват на различни стойности на параметър. Според (75.11) и (75.12), отколкото по-малко. тези по-горе и в дясно на тази крива е максимален. При много високо затихване (като това) на експресията на резонансна честота става въображаема. Това означава, че при тези условия не се наблюдава резонанс - с увеличаване на честотата на амплитудата на принудени трептения се намалява монотонно (виж долната крива на фигура 189 ..). показано на
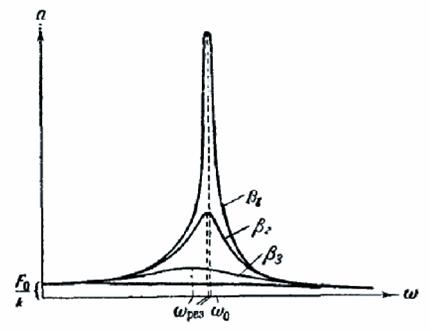
Фиг. 189 набор от графики на функции (75.7), съответстващи на различни стойности на параметъра. Той призова резонансни криви.
Що се отнася до криви резонанс може да направи следните забележки. Клони към нула, всички криви достигнат до същото различна от нула, на граничната стойност, равна. т. е. F 0 / к. Това се компенсира от равновесното положение, което получава на системата при постоянна сила на величина F 0. В стремежа си да безкрайност, всички криви асимпотично доближават нула, тъй като високата честота на властта толкова бързо сменя посоката си, системата не успява да забележимо се премине от равновесното положение. Накрая, имайте предвид, че колкото по-малка. силния C варира близо до резонансната честота на амплитудата, на "-остър" се получава макс.
От формула (75,12) следва, че за ниско затихване (т. Е. В) амплитуда в резонанс е приблизително равна на
Разделете този израз XQ изместване от равновесното положение под действието на постоянна сила F 0. равни, като открихме. Резултатът:
[V. формула (73,13)]. По този начин качеството на фактор Q на показва колко пъти амплитудата в точката на резонанс надвишава системата компенсира от неговата равновесна позиция под действието на постоянна сила на същата величина като амплитудата на силата на движение (това е вярно само за малка затихване).

Както се вижда от фиг. 187, принудени трептения изостава движещата сила със стойността на закъснение е в границите от 0 до. Зависимостта от най-различни стойности е показана графично на Фиг. 190. честота съответства. Най-резонансната честота по-малко от естественото [виж. (75,11)]. Ето защо, по време на резонанс. Когато слабо затихване. Стойност 0 в резонанс, може да се разглежда като равен.
С явлението резонанс трябва да се съобразяваме при проектирането на машини и всички видове строителство. Собствената честота на вибрациите на тези устройства в никакъв случай не трябва да бъде в близост до Честотата на възможните външни влияния. Така например, естествената честота на вибрациите на корпуса или крилото на самолета трябва да е много по-различна от честота на трептене, което може да се вълнува от въртенето на витлото или витлата. В противен случай, вибрации се появяват което може да доведе до катастрофа. Има случаи, когато засегнати от мостове, когато се преминава от тях маршируващи колони от войници. Това е така, защото естествената честота на трептене на моста е близо до честотата, с която пристъпи колоната.
Bmeste с феномена резонанс често е много полезно, особено в акустика, радио и др. Г.