Начин на възли в проблем В5

Има една прекрасна формула, която ни позволява да се помисли за района на полигон на стартовата решетка с почти никакви грешки. Той дори не е формула, а настоящото теорема. На пръв поглед може да изглежда обезсърчително. Но това е достатъчно, за да се реши няколко проблема - и ще видите как тази страхотна функция. Така че продължавайте напред!

За да започнете, ще се въведе нова дефиниция:

Node координира купчини - е всяка точка, разположена на пресичането на вертикалните и хоризонталните линии на решетката.

В първата картина възли обикновено не са маркирани. 4 са определени при втория възел. И накрая, всички 16 единици са отбелязани на третия снимката.

Как това се отнася до проблем В5? Фактът, че върховете на многоъгълника в такива проблеми са винаги в окото възли. В резултат на това, те работят следната теорема:

Теорема. Помислете за полигон мрежа, чиито върхове лежат по възлите на мрежата. Тогава площта на полигона, е равна на:

където п - броят на възли в рамките на даден многоъгълник, к - броят на възлите, които се намират на границата (гранични възли).

Като пример, помислете за редовна триъгълник на стартовата решетка и се опитват да се отбележи, вътрешните и граничните възли.

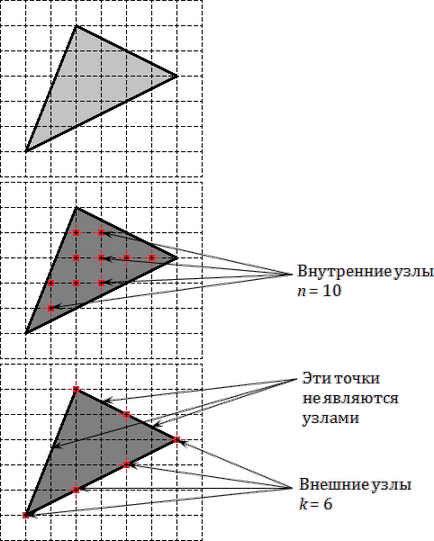
Първото изображение се дава редовно триъгълник. На втория маркиран своите вътрешни компоненти, броят на които е равна на п = 10. На трето картина отбелязани възли, разположени на границата, има само к = 6.

Вероятно много читатели не разбират как да се преброят н и к. Започнете с вътрешни възли. Всичко е ясно: нарисува триъгълник молива и да видим как много сайтове бяха подложени на засенчване.

С малко по-сложни гранични възли. Границата на полигона - затворена начупена линия. който пресича стартовата решетка на много места. Най-лесният начин е да се отбележи всеки "изходен" точка, а след това се заобиколят останалите.

Гранични възли са само тези точки по прекъснатата линия, където се пресичат три линии в същото време.

1. В действителност, прекъсната линия;
2. Хоризонталната линия на мрежата;
3. Вертикалната линия.

Нека да видим как тя работи в тези задачи.

Задача. Намерете област триъгълник, ако размерът на клетка е 1 х 1 см:

Да започнем с възли, които се намират във вътрешността на триъгълника, както и по границата си:

Оказва се, че само един вътрешен възел: п = 1. гранични възли - толкова, колкото шест, три съвпадат с върховете на триъгълника. и трите са от двете страни. Общо к = 6.

А сега да разгледаме района с помощта на формулата:

Това е! Проблемът е решен.

Задача. Виж областта на четириъгълник, показано на милиметрова хартия с размера на клетката на 1 см от 1 см. Response до получаване квадратни сантиметра.

Отново, ние се отбележи, вътрешните и граничните възли. Вътрешни възли на всички п = 2. Гранични възли: к = 7, 4 от които са върховете на четириъгълник. и още 3 са от двете страни.

Остава да замени номера н и к във формулата за площ:

Важна забележка на областите

Но формулата - това не е всичко. Нека да пренапише формулата, носейки отношение на правото на общ знаменател. получаваме:

номера н и к, - е броят на възли, те винаги са числа. Така че, също цяло числител. Ние го разделете на две, което означава един важен факт:

Районът винаги се изразява като цяло число или фракция. А в края на фракцията е винаги "пет десети": 10,5; 17,5 и т.н.

Така, в В5 проблемна област винаги се изразява като цяло число или част от формата *** 5. Ако отговорът е различен, това означава, че някъде грешка. Имайте това предвид, когато се взема реалния изпит по математика!

• Безплатна Подготовка за изпита 7 прости, но много полезни уроци + домашна работа
•