Принудително механични трептения 1

Означаваме - ъгълът между обем и сила за управление.

Заместването (3.3.3), (3.3.4) и (3.3.5) до (3.3.1):

Всеки термин в последната формула може да бъде представена като съответната амплитудата на въртящите вектори:

- ускорение амплитуда; - амплитуда на скоростта; - амплитуда на преместване; - амплитудата на движеща сила. и

принуди амплитуда вектор намерени в принципите на допълнение вектор:

.

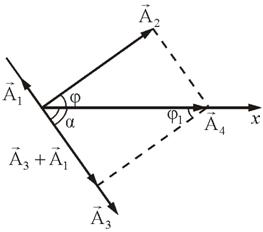
Фиг. 3.2 показва, че. Ние считаме, амплитудата А:

.

По този начин, и двете.

При постоянна F0. β м, а амплитудата зависи само от съотношението на ъглова честота ω на движеща сила и свободни незатихващи трептения ω0 система.

В началната фаза на принудени трептения могат да бъдат намерени от израза

Фиг. 3.3 показва, че силата напред на отклонението под ъгъл, който се определя с израза

.

1) (честотата на движещата сила е нула), тогава

- статичен амплитуда (вибрации не се срещат).

2) (без затихване). С увеличаване на со (но) амплитуда нараства и рязко се увеличава (). Това явление се нарича резонанс. По-нататъшно повишаване на со () амплитуда намалява отново (фиг. 3.4).

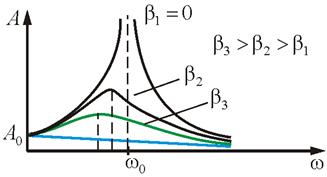
3) амплитудата ще бъде максимум на минималната стойност на знаменател. За да намерите точките на инфлексия вземат първата производна на ω radicand (3.3.7) и да го настроите да е равна на нула:

4ω ≠ 0, и следователно, изразът в скоби е равна на нула: