Площта на трапец - формула, примери за изчисление

Trapeze нарича четириъгълник, в който само две страни, успоредни една на друга.

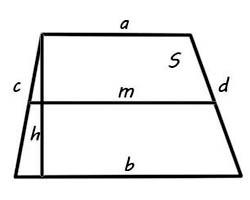
Те се наричат основи на отделните фигури, останалите - фланговете. Специални случаи на форма успоредник се вземат под внимание. Има и криволинейна трапец, която включва графика на функцията. Трапецoвидната форма правило области включват почти всички от неговите елементи, и най-доброто решение е избран в зависимост от зададените стойности.

Главната роля в разгара на прибиране на трапеца и средната линия. В средната линия - линия, свързваща средата на двете страни. Височината на трапеца се провежда под прав ъгъл от горния ъгъл към основата.
Площта на трапец през височина, равна на произведението на половин сумата от дължините на основите пъти височината:

Ако е известно, в условията на средната линия, тази формула е много опростен, тъй като тя е равна на половината на сбора от дължините на основите:

Ако условията са дадени дължините на страните, можете да видите пример за изчисляване на площта на трапец през тази информация:

Да приемем, даден трапец с основи а = 3 см, В = 7 см и странични страни в = 5 см, D = 4 см определят зоната на фигурата .:

Площта на равностранен трапец

Отделен случай е равнобедрен, или, както го наричат, равнобедрен трапец.
Специален случай е определянето на областта на равнобедрен (равностранен) трапец. Формула показва по различни начини - чрез диагонал през ъглите, съседни на основата и радиуса на вписан кръг.
Ако условията, дадени диагонал дължина и известни ъгъл може да се използва следната формула между тях:

Не забравяйте, че диагоналите на един равностранен трапец са равни!

На следващо място, нека разгледаме още един пример за изчисляване на площта на равнобедрен (равностранен) трапец. Формула от страна и в близост до основата на ъглите направи лесно да се намери областта на фигурата.

Това означава, че знае една от техните бази, площта на страна и ъгъл може лесно да бъде изчислено.

Площта на криволинеен трапец

Отделен случай - криволинейна трапец. Той е разположен на координатните оси и се ограничава да планирате продължително позитивно функция.

Нейната база е разположена по оста X и се ограничава до две точки:
Integrals помогнат изчислява площта на криво трапец.
Формулата е предписано, както следва:

Вземем примера на изчисляване площта на криво трапец. Формулата изисква известни познания за работа с определени интеграли. За да започнете, ние анализираме стойността на определен интеграл:

Когато F (а) - тази стойност примитивна функция е (х) на точка. F (б) - стойността на F функция (X) в точка б.

Сега ние решаване на проблема. Фигурата показва криво трапец, ограничена функция. функция
Трябва да намерим областта на избраната форма, която е извита трапец топ ограничено график на правилните линии х =, наляво линии х = OX и оста на дъното.
Площта на тази цифра, ние ще разчитаме на следната формула:

Условия за проблема ни е дадено функция. На него откриваме примитивна стойност във всяка от нашите точки:

сега
Отговор: В района има предвид криволинеен трапец е равна на 4.

Нищо сложно при изчисляването на тази стойност не е налице. Важно незначително внимание в изчисленията.